Home page of

                                                                       

HENK HILHORST

                                                                                                 
 

Address:       Laboratoire de Physique Théorique
                       Bâtiment 210
                       Université de Paris-Sud
                       91405 Orsay
                       France
Telephone:       (0)1 6915 7787
Fax:                  (0)1 6915 8287
E-mail:         Henk Hilhorst
 
 
 

Research

Publications   .pdf   .ps     (last update December 2014)

/This page is under construction and will be expanded. References will be added./
/Last update October 29, 2010./
 
 

                    Voronoi tessellations


 
       

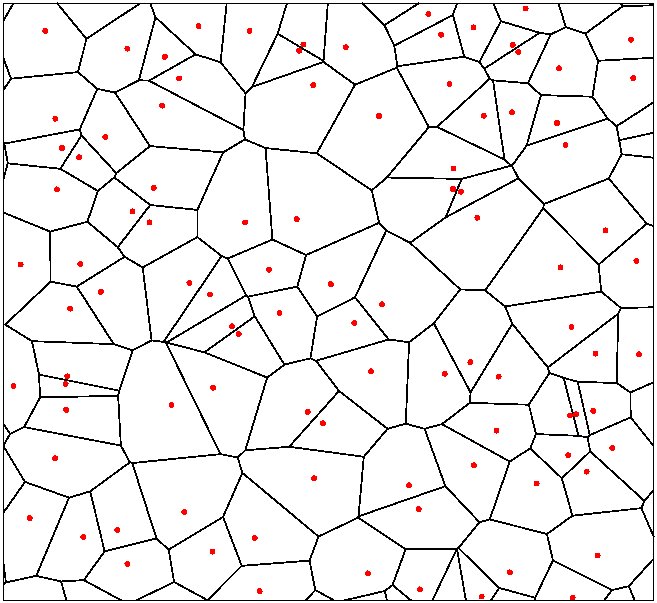
The three figures on the left represent what is called Poisson-Voronoi tessellations.

The red dots are the "centers", randomly and uniformly distributed in the plane with unit density [mathematicians say that they are a Poisson process of intensity 1].
The black lines partition the plane into cells, one cell for each center, in such a way that each generic point of the plane is in the cell of the center to which it is closest. These cells are called Voronoi cells and the cell diagram is called a tessellation (in French: un pavage ou une mosaïque).

Figure 1 is just a statistically average tessellation. You see that the Voronoi cells come in many different shapes and sizes. In particular, they have a variable number of sides. The probability distribution of this number of sides -- let's call it n -- is a quantity of interest.

    
Figure 1

 
 

   
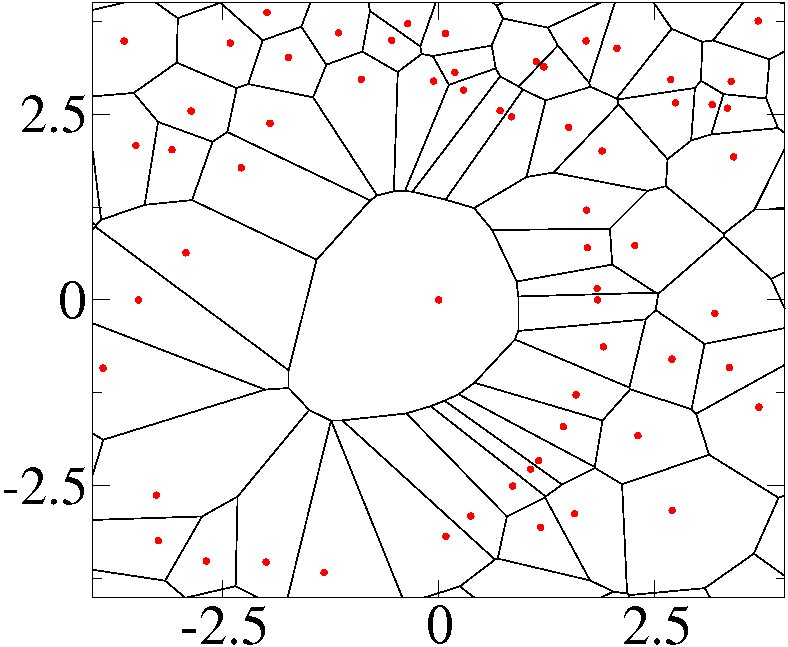
Figure 2 is a very exceptional tessellation in which there occurs a cell that is 24-sided! Such events are extremely rare. They have been the subject of my research in the period 2005-2008. Let us call pn the probability that a cell randomly picked from a tessellation have n=24 sides. For n=24 we have that p24 is only about 10-18.

It is remarkable that most of the first-neighbor cells of the 24-sided "central" cell are quite elongated. This feature will become more and more pronounced when we increase the number of sides n.

   
Figure 2

 
 

   
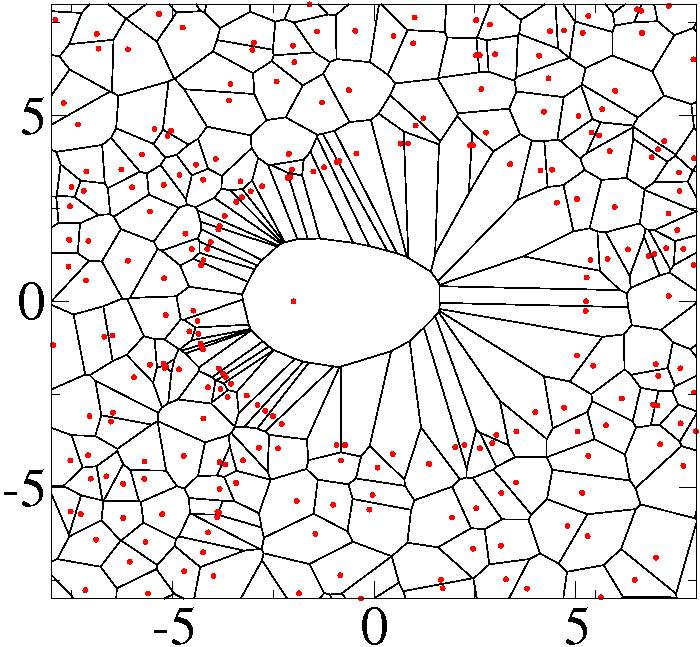
Figure 3 is even more exceptional than Figure 2. A cell occurs that is 48-sided! The probability for a cell to have 48 sides is only about 10-60. But if it does occur, it will look like shown in the figure.

   
Figure 3